Artikel

Perl

• Charsets und Unicode
• Rezension "Higher Order Perl"
• Perls Schwächen

Algorithmen

• Rekursion
• Verkettete Listen in C
• Doppelt verkettete Listen in C
• Heaps und Heapsort in C und C++

Doppelt verkettete Listen in C

Doppelt verkettete Listen (oder doubly linked lists) sind häufig benutze Datenstrukturen und eine Verallgemeinerung der einfach verketteten Listen, die ich hier anhand von Beispielen in der Programmiersprache C vorstellen will.

Sie funktioniert in jeder Programmiersprache genauso, die Zeiger oder Referenzen und so etwas wie Klassen oder Structs zur Verfügung stellt.

Was bringen doppelt verkettete Listen?

Doppelt verkettete Listen, oder "double linked lists" braucht man immer dann, wenn man sich in einer Liste leicht vorwärts und rückwärts bewegen können muß, und wenn man schnell und einfach Elemente der Liste an beliebigen Positionen löschen und neue einfügen muß.

Ein Beispiel ist z.B. die Implementierung Spärlich besetzter Matrizen ("Sparse Matrices"), aber es gibt viele weiter Anwendungen.

Die Grundidee

Die Idee einer doppelt verketteten Liste ist es, für jedes Element zwei Zeiger zu speichern, einen nach links und einen nach rechts:

struct node {
	struct node *left;
	struct node *right;
	int data;
};

Die eigentlichen Daten, die in der Liste gespeichert werden sollen, stehen in data, das hier als int definiert ist. Jeder andere Datentyp, z.B. ein Zeiger auf beliebige andere Strukturen, funktioniert genau so.

Die Illustrationen weiter unten werden dazu beitragen, die Struktur verständlich zu machen.

Eine Liste erzeugen

Eine Liste ist nichts anderes als ein einzelnes Element, das auf sich selbst zeigt. Mit diesem Wissen kann man eine neue Liste erzeugen:

struct node * new_list(){
	struct node *new = (struct node*) malloc(sizeof(struct node));
	new->data  = -1;
	new->right = new;
	new->left  = new;
	return new;
}

(Anmerkung: In C++ darf man die Variable nicht new nennen, da das ein reserviertes Wort ist).

Dadurch, dass das erste Element auf das letzte zeigt und umgekehrt, kann man sich bei den späteren Operationen Abfragen ersparen, ob man bei dem letzten Element angekommen ist.

Oft empfiehlt es sich, dem ersten Element einen Wert zu geben, den die anderen Elemente nicht annehmen können, z.B. -1 wenn alle anderen Elemente größer gleich Null sind.

Elemente einfügen

Jetzt kommt der eigentliche Vorteil doppelt verketteter Listen zum tragen: das Einfügen neuer Elemente ist sehr einfach:

struct node * insert_right(struct node *list, int data){
	struct node *new = (struct node *) malloc(sizeof(struct node));
	new->data        = data;
	new->left        = list;
	new->right       = list->right;
	list->right      = new;
	new->right->left = new;
	return new;
}

Die Schritte im einzelnen:

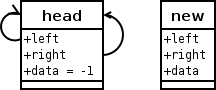
Ein neues struct node wird erstellt und die Daten werden initialisierst.

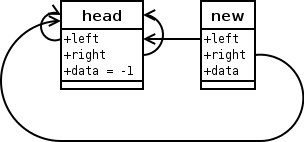
Die Zeiger des neuen Elements werden gesetzt.

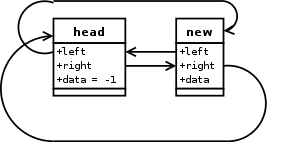
Der Zeiger right des Elements auf der linken Seite wird auf das neue Element gesetzt, ebenso der Zeiger left des Elements auf der rechten Seite des neu eingefügten Elements.

Noch ein Beispiel für das Einfügen

Da das vorherige Beispiel ein Spezialfall einer Liste mit nur einem Element war, hier noch ein Beispiel, diesmal mit einer zweielementigen Liste, in die ein drittes Element rechts neben head, also in der Mitte eingefügt werden soll.

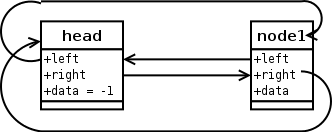
Eine doppelt verkettete Liste mit zwei Elementen.

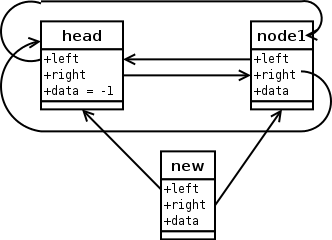
Ein neues Objekt wird erstellt, der Zeiger new->left wird auf head gesetzt, der Zeiger new->right wird auf head->right gesetzt, was gleichbedeutend mit node1 ist.

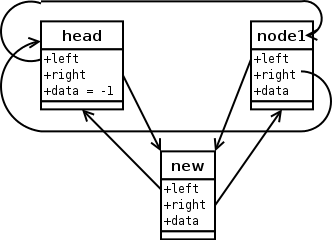
Der Zeiger head->right wird auf new gesetzt. Jetzt muss noch node1->left auf new gesetzt werden, aber da wir keinen Zeiger mehr von head aus auf node1 haben, ist der einfachste Weg über new->right: new->right->left = new.

Und schon sind wir fertig - mit dem umbiegen von nur vier Zeigern.

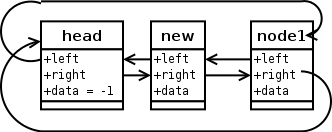
Hier noch einmal die gleiche Liste, diesmal mit dem neuen Element auf gleicher Höhe wie die anderen Elemente. Sieht doch gleich viel übersichtlicher aus...

top

Elemente Löschen

Für viele Backtracking-Algorithmen ist es hilfreich, wenn man Elemente schnell entfernen und gegebenenfalls wieder einfügen kann. Hier erst mal der codes fürs löschen:

struct node * delete(struct node *list){
	list->right->left = list->left;
	list->left->right = list->right;
	return list->left;
}

Am Beispiel:

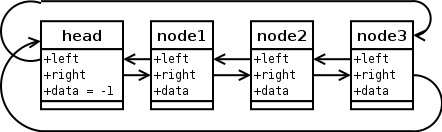
Aus dieser Liste soll node2entfernt werden, es wird also delete(node2)aufgerufen.

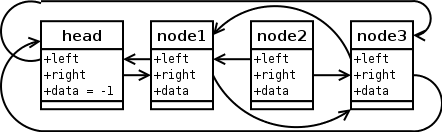
list->right->left, also node3->left, auf den linken Nachbarn des zu löschenden Elements gesetzt, also auf node1. Danach kommt die andere Richtung dran, d.h. list->left->right, also node1->right, wird auf den rechten Nachbarn des zu löschenden Elements gesetzt, also auf node3.

Wenn man sich jetzt von head aus an den Zeigern entlang durch die Liste hangelt, erreicht man node2 nicht mehr, das Element ist also quasi gelöscht.

Allerdings wird in Funktion den Speicher, den node2, oder wie es innerhalb der Funktion heißt, list benötigt, nicht wieder freigegeben, denn es können ja noch andere Zeiger auf dieses Element existieren.

Und wenn man das Element nicht löscht, kann man es später wiederherstellen, wenn man noch einen Zeiger darauf hat.

Elemente wiederherstellen

Gelöschte Elemente, auf die man noch einen Pointer hat, können sehr einfach wieder in die Liste eingefügt werden:

struct node * restore(struct node *list){
	list->right->left = list;
	list->left->right = list;
	return list;
}

Das ist sogar noch weniger Aufwand als das Einfügen, da zwei der Zeiger schon richtig gesetzt sind, und zwar die in dem wiederherzustellendem Element.

Die Liste durchlaufen

Es ist sehr einfach, die doppelt verkettete Liste nach rechts oder links zu durchlaufen, man muss lediglich darauf aufpassen, dass man nach einem Durchlauf aufhört.

Hier ein Beispiel zur Ausgabe einer Liste:

void print_all(struct node* list){
	struct node *head = list;
	struct node *current = list;
	printf("%d ", head->data);
	while (head != (current = current->right)){
		printf("%d ", current->data);
	}
	printf("\n");
}

Hier wird das erste Element der übergebenen Liste in der Variable head gespeichert, und current läuft durch die Liste, in diesem Fall nach rechts.

Wenn beide wieder gleich sind, d.h. die Liste einmal vollständig durchlaufen ist, wird die Schleife beendet.

Ein kleines Testprogramm

Zeit, die geschriebenen Funktionen zu testen:

int main(int argc, char** argv){
	/* erstelle eine neue Liste: */
	struct node *head    = new_list();
	struct node *current = head;
	int i;

	/* Befuelle die List mit den Zahlen 1 bis 10 */
	for(i = 1; i <= 10; i++){
		current = insert_right(current, i);
	}

	/* Gebe die Liste  aus, einmal von head aus startent, einmal vom 
	   letzten Element aus: */
	print_all(head);
	print_all(current);

	/* loesche das vorletzte Element: */
	current = current->left;
	current = delete(current); 
	printf("Liste nach loeschen:\n");
	print_all(head);

	current = delete(head);
	printf("Liste nach loeschen des Kopfes:\n");
	print_all(current);

	head = restore(head);
	printf("Liste nach Wiederherstellen des Kopfes:\n");
	print_all(head);

	return 0;
}

Und die passende Ausgabe dazu:

-1 1 2 3 4 5 6 7 8 9 10 
10 -1 1 2 3 4 5 6 7 8 9 
Liste nach loeschen:
-1 1 2 3 4 5 6 7 8 10 
Liste nach loeschen des Kopfes:
10 1 2 3 4 5 6 7 8 
Liste nach Wiederherstellen des Kopfes:
-1 1 2 3 4 5 6 7 8 10

Offensichtlich funktionieren die Funktionen wie gewünscht.

Mögliche Probleme

Hier sei noch auf ein paar Fehler hingewiesen, die man vermeiden sollte:

Endlosschleifen

Was macht folgender Code?

delete(current);
print_all(current);

Das Element current wird gelöscht, und anschließend wird die Liste ausgegeben.

Prinzipiell sollte das funktionieren, schließlich sind in dem entfernten Element noch Zeiger auf den Rest der Liste gespeichert. Allerdings erzeugt man damit eine Endlosschleife in der Funktion print_all, da diese solange läuft, bis sie zum ursprünglichen Element zurückkommt.

Da das Element aber nicht von der Liste aus erreichbar ist, wird die Liste so oft ausgegeben, bis der Benutzer das Programm abbricht.

Daraus kann man sich folgende Regel herleiten:

Mit entfernten Elementen einer Liste darf man nichts anderes machen, als restore aufzurufen.

Memory Leaks

Was macht folgender Code?

current = insert_right(current, 2);
current = delete(current);

Nun, erst wird ein Knoten mit dem Wert 2 eingefügt, und dann wird er wieder entfernt, die Liste ist weiterhin intakt.

Allerdings wurde in insert_right ein Stück Speicher für das neue Element reserviert, auf den es keinen Pointer mehr gibt, der aber auch nicht frei geworden wurde.

Wenn das mehrfach in den Programm passiert, läuft der Speicher mit nutzlosen Daten voll.

Abhilfe schafft es, das Element mit free() zu löschen und den Speicher an das Betriebssystem zurückzugeben:

current           = insert_right(current, 2);
struct node * tmp = current;
current           = delete(current);
free(tmp);
tmp        = NULL;

Wenn das häufiger vorkommt, ist es sinnvoll eine Funktion delete_and_free zu schreiben, die das gelöschte Element automatisch frei gibt:

struct node * delete_and_free(struct node *list){
	list->right->left = list->left;
	list->left->right = list->right;
	struct node *res  = list->left;
	free(list);
	return list->left;
}

Diese beiden Probleme, Endlosschleifen und Memory Leaks, kann man umgehen, indem man die Datenstruktur weiter kapselt und als Interface z.B. immer nur head und einen aktuellen Zeiger anbietet.

Allerdings verliert man damit auch ein wenig Funktionalität.

Löschen und wiederherstellen mehrerer Elemente

Man betrachte eine Liste aus einem Kopf und drei Elementen node1, node2 und node3, aus der das zweite Element gelöscht wird:

Und jetzt lösche man node1:

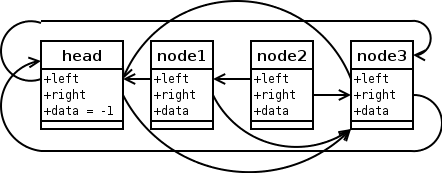
Das sieht nicht mehr so schön aus. Wenn man jetzt erst node1 und dann node2 wieder herstellen, sind wir wieder bei der ursprünglichen Liste.

Aber was passiert, wenn man erst node2 wiederherstellt?

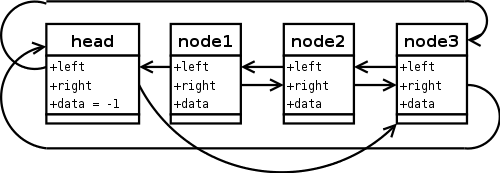
Die Antwort ist, dass ein Zeiger von dem gelöschten node1 anstatt von head auf das wiederhergestellte Element verbogen wurde, das Resultat ist keine gültige, doppelt verkettete Liste.

Aus diesem Beispiel kann man sich eine Regel herleiten:

Gelöschte Elemente dürfen nur in umgekehrter Reihenfolge wiederhergestellt werden.

Zusammenfassung

Die meisten Operationen auf doppelt verketteten Listen bestehen aus dem umsetzen von einem bis vier Zeigern; solange man die Übersicht bewahrt und sich vorher aufmalt, welche Zeiger wohin müssen, sind die Operationen auch nicht kompliziert.

Das bewegen in der Liste sowie das Einfügen und Löschen von Elementen geht jeweils sehr schnell, nur der Zugriff auf ein Element mit einer bestimmten Nummer - was die Stärke von Arrays ist - erfordert das Durchlaufen der einzelnen Elemente.

Weiteres Lesematerial

• Einfach verkettete Listen
• Heaps und Heapsort

Bücher

"Algorithmen in C" von Robert Sedgewik ist allgemeinverständlich und praktisch. "The Art of Computer Programming" von Donald Knuth ist ein Klassiker, und beschreibt für den mathematisch interessierten Leser Algorithmen, Datenstrukturen und ihre Vor- und Nachteile im Detail (Englisch).