Artikel

Perl

Algorithmen

Heaps und Heapsort in C

Ein Heap, auf Deutsch auch Haldenspeicher gennant, ist eine Datenstruktur, die Daten sortiert und kompakt speichert und schnelles Einfügen und Löschen zulässt. Sie ist damit für das Sortieren von Daten und als Prioritätswarteschlange (priority queue) sehr gut geeignet ist.

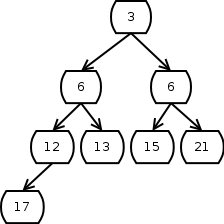
Ein Heap ist ein Binärer Baum, dessen Elemente eine bestimmte Ordnung einhalten, und der dicht gefüllt ist.

Genauer gesagt sind Elemente des Heaps so angeordnet, dass die Kinderelemente immer größer oder gleich dem Vaterelement sind.

Außerdem unterscheidet sich die Höhe des Baums an zwei beliebigen Stellen maximal um eins, der Baum ist also immer ausbalanciert.

Arbeiten mit dem Heap

Wenn man einen Heap bearbeitet, verändert man meistens ein Element, und stellt dann die Heapbedingungen wieder her.

Einfügen eines Elements

Zum Einfügen eines Elements wird das neue Element zuerst am Ende angehängt, d.h. Wenn die unterste Ebene voll ist, ganz links an den Baum, wenn nicht in die letzte Zeile so weit links wie möglich.

Danach wird die Heap-Bedingung wieder hergestellt. Dazu geht man von dem neu eingefügtem Element aus nach oben bis zur Spitze des Baums, und wenn an einer Stelle das Vaterelement größer als das Kindelement ist, werden die beiden Elemente vertauscht.

Als Beispiel wird im Beispiel von vorher eine 4 eingefügt:

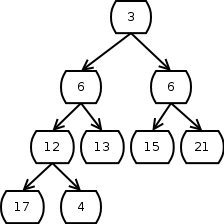
Um die Heapbedingung wieder herzustellen, wird das neu eingefügte Element mit seinem Vaterelement, der 12, verglichen. Da es kleiner ist als das Vaterelement, werden die beiden vertauscht:

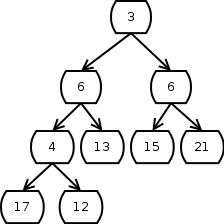
Jetzt wird die 4 mit dem Vaterelement, der 6, verglichen. Wieder ist es kleiner, die beiden Elemente werden vertauscht.

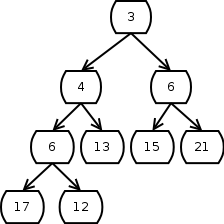
Die 4 wird mit dem Vaterelement, der 3, verglichen. Die 4 ist größer, das heißt alles ist in Ordnung, die Heap-Bedingung ist wieder hergestellt.

Die Anzahl der Vergleiche und Vertauschung ist proportional zur Höhe des Baums, und damit zum Logarithmus der Anzahl der Elemente.

Das Wurzelelement entfernen

Die zweite häufig gebrauchte Operation ist das Entfernen des Wurzelelements, also des kleinsten Elements im Heap.

Dazu wird das letzte Element an die Stelle des Wurzelelements kopiert, und danach wird die Ordnung des Heaps wieder hergestellt.

Um beim vorherigen Beispiel zu bleiben, wird die 3 an der Spitze (also das Wurzelelement) gelöscht, und das letzte Element, die 12, an dessen Stelle verschoben.

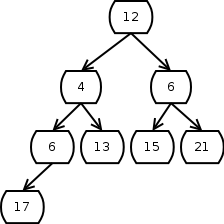
Zum Wiederherstellen der Heapbedingung wird das Wurzelelemnt mit den beiden Kinderelementen verglichen, und, wenn es größer ist als eines der beiden Kinder, wird es mit dem kleineren Kindelement getauscht.

In diesem Fall wird die 12 mit dem linken Kind, der 4, vertauscht:

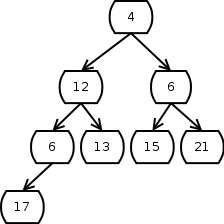
Jetzt ist die 12 größer als die 6, mit der sie vertauscht wird.

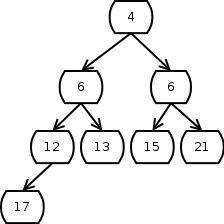
Die Zwölf ist jetzt kleiner als das einzige Kindelement, die 17, d.h. die Heapbedingung ist wieder hergestellt.

Die Anzahl der Vergleiche und Vertauschungen ist wie beim Einfügen proportional zur Höhe des Baumes.

Heapsort: Sortieren mit Heaps

Wenn man schon einmal ein Heap implementiert hat, ist es sehr einfach, mit dessen Hilfe effizient zu sortieren.

Man schiebt einfach alle zu sortierenden Elemente in den Heap, und entfernt dann immer wieder das Wurzelelement.

Da das Wurzelelement immer das jeweils kleinste Element des Heaps ist, erhält man die Zahlen in aufsteigender Reihenfolge aus dem Heap.

Dieser Algorithmus wird Heapsort genannt.

Wenn der Heap n Elemente enthält, braucht man für das Einfügen und Entfernen log(n) Operationen, das heißt das Sortieren von n Element braucht O(n*log(n)) Operationen.

Damit ist die asymptotische Laufzeit optimal (das Problem des vergleichsbasierten Sortierens lässt sich nicht schneller als in O(n * log(n)) Schritten lösen). Auch in der Praxis ist Heapsort schnell, aber für die Cache-Architekturen moderner Computer nicht unbedingt optimal, weshalb für große Datenmengen üblicherweise Mergesort oder Quicksort einsetzt.

Implementierung

Auch wenn man einen Heap mit Zeigern aufbauen kann, so ist es doch sehr viel Aufwand, und das Einfügen und Entfernen von Elementen ist recht aufwändig.

Wenn man die maximale Größe des Heaps im Voraus kennt, speichert man ein Heap deswegen gerne in einem Array. Damit spart man sich den Platz für die Pointer, und benutzt den Array-Index als Ersatz für den Pointer.

Dabei speichert man die Wurzel an der Stelle 1, und die beiden Nachfolger des Knotens n an den Stellen 2n und 2n+1:

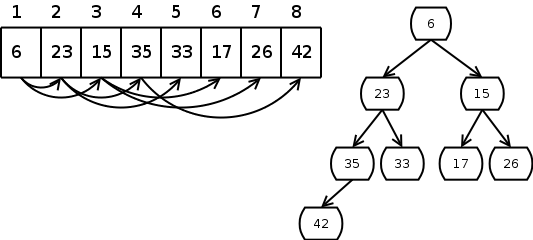
Lese- und Schreiboperationen auf Arrays sind billig, d.h. wenn man vorher die Größe kennt ist das Array am besten geeignet.

Im folgenden wird davon ausgegangen, dass es ein Array names heap gibt sowie ein integer heap_p, der auf das letzte Element des Heaps zeigt.

Element einfügen

Zum Einfügen wird das Element einfach an das Ende kopiert, und dann die Heapbedindung wieder hergestellt:

void push(int item){
    heap_p ++;
    heap[heap_p] = item;
    reheap_up(heap_p);
}

void reheap_up(int pointer){
    int p = pointer;
    int new_p = p / 2;
    while (p > 1 && heap[new_p] > heap[p]){
        /* swap the two elements */
        int tmp = heap[new_p];
        heap[new_p] = heap[p];
        heap[p] = tmp;
        p = p / 2;
        new_p = new_p / 2;
    }
}

Die Funktion reheap_up geht den Heap von dem gegeben Element pointer aus bis zur Spitze (oder bricht vorher ab wenn die Heap-Bedingung wieder hergestellt ist), und vertauscht die beiden übereinanderliegenden Elemente, falls das obere Element größer ist als das untere.

Wurzelknoten löschen

Auch das Löschen des Wurzelelements ist nicht sehr kompliziert:

int pop(void){
    int res = heap[1];
    heap[1] = heap[heap_p];
    heap_p--;
    reheap_down(1);
    return res;
}

Die hier verwendete Funktion reheap_down(int) startet von einem gegebenen Element aus, und geht von dort aus nach unten durch den Baum und stellt dabei die Heap-Bedingung wieder her:

void reheap_down(int pointer){
    int new_p;
    if (2 * pointer > heap_p){
        return;
    }
    if (2 * pointer + 1 <= heap_p
            && heap[2*pointer+1] < heap[2*pointer]){
        new_p = 2 * pointer + 1;
    } else {
        new_p = 2 * pointer;
    }
    if (heap[pointer] > heap[new_p]){
        int tmp = heap[pointer];
        heap[pointer] = heap[new_p];
        heap[new_p] = tmp;
        reheap_down(new_p);
    }
}

Implementierung in C++

Einen Heap kann man sehr schön in einer Klasse kapseln, wofür sich C++ wiederum eignet. Hier eine sehr einfache Implementierung.

Diese Implementierung unterscheidet sich von der Logik her nicht von der vorherigen, hat aber ein saubereres Interface.

myheap.hpp

#ifndef _MYHEAP_HPP_
#define _MYHEAP_HPP_

class myheap {
    public:
        // Erstelle einen neuen Heap mit mix. size Elementen
        myheap(int size);
        // Erstelle einen Heap aus dem Array a[] mit size Elementen
        myheap(int a[], int size);

        ~myheap();

        // Lege item auf dem Heap ab
        void push(int item);

        // entferne den Wurzelknoten und liefere das Element
        // zurück
        int pop(void);

    protected:
        int *data;
        int pointer;

        void reheap_up(int start);
        void reheap_down(int pointer);
        void reheap_all();

        void check_heap_condition(void);
};

#endif

Die Funktion check_heap_condition dient nur der Kontrolle der Implementierung und kann auch weggelassen werden.

myheap.cpp

#include "myheap.hpp"
#include <stdlib.h>
#include <stdio.h>

myheap::myheap(int size){
    data = new int[size + 2];
    pointer = 0;
}

myheap::myheap(int *a, int size){
    data = new int[size + 2];
    for (int i = 0; i < size; i++){
        data[i+1] = a[i];
    }
    pointer = size;
    reheap_all();
}

myheap::~myheap(){
    delete[] data;
}


void myheap::push(int item){
    pointer ++;
    data[pointer] = item;
    reheap_up(pointer);
}

void myheap::reheap_up(int start){
    int p =start;
    int new_p = p / 2;
    while (p > 1 && data[new_p] > data[p]){
        /* swap the two elements */
        int tmp = data[new_p];
        data[new_p] = data[p];
        data[p] = tmp;
        p = p / 2;
        new_p = new_p / 2;
    }
}

void myheap::reheap_all(){
    int p;
    for (p = 1; p <= pointer; p++){
        reheap_up(p);
    }
}


void myheap::reheap_down(int pointer){
    int new_p;
    if (2 * pointer > this->pointer){
        return;
    }
    if (2 * pointer + 1 <= this->pointer
            && data[2*pointer+1] < data[2*pointer]){
        new_p = 2 * pointer + 1;
    } else {
        new_p = 2 * pointer;
    }
    if (data[pointer] > data[new_p]){
        int tmp = data[pointer];
        data[pointer] = data[new_p];
        data[new_p] = tmp;
        reheap_down(new_p);
    }
}

int myheap::pop(void){
    int res = data[1];
    data[1] = data[pointer];
    pointer--;
    reheap_down(1);
    return res;
}

void myheap::check_heap_condition(void){
    int i;
    for (i = 2; i <= pointer; i++){
        if (data[i/2] > data[i]){
            printf("\nError at index %d, %d\n", i, i/2);
            exit(1);
        }

    }

}

Ein kleines Testprogramm

Ein kleines Programm soll demonstrieren, dass der Heap tatsächnlich funktioniert:

#include <iostream>
#include "myheap.hpp"

using std::cout;

int main(int argc, char** argv){
    int a[8] = {1, 6, 8, 3, 2, 7, 3, 4};
    myheap h1(a, 8);
    for (int i = 0; i < 8; i++){
        cout << h1.pop() << "\n";
    }

    return 0;
}

Kompilieren: Makefile

Zum kompilieren, hier mit g++, dem C++-Kompiler der Gnu Compiler Collection, eine kleine Makefile:

CC=g++
LDFLAGS=-lm
CFLAGS=-pipe -Wall -ansi -pedantic -g -O1
OBJECTS=myheap.o
BIN=myheap

.SUFFIXES: .cpp 

.cpp.o: 
	$(CC) $(CFLAGS) -c $< 

$(BIN): $(OBJECTS) main.cpp
	$(CC) $(CFLAGS) $(LDFLAGS) -o $(BIN) main.cpp $(OBJECTS)

clean:
	rm -f $(OBJECTS) $(BIN) core

Download

Die obigen Dateien gibt es auch zum herunterladen (als .tar.gz Archiv).