Categories
Posts in this category
- Current State of Exceptions in Rakudo and Perl 6
- Meet DBIish, a Perl 6 Database Interface
- doc.perl6.org and p6doc
- Exceptions Grant Report for May 2012
- Exceptions Grant Report -- Final update
- Perl 6 Hackathon in Oslo: Be Prepared!
- Localization for Exception Messages
- News in the Rakudo 2012.05 release
- News in the Rakudo 2012.06 release
- Perl 6 Hackathon in Oslo: Report From The First Day
- Perl 6 Hackathon in Oslo: Report From The Second Day
- Quo Vadis Perl?
- Rakudo Hack: Dynamic Export Lists
- SQLite support for DBIish
- Stop The Rewrites!
- Upcoming Perl 6 Hackathon in Oslo, Norway
- A small regex optimization for NQP and Rakudo
- Pattern Matching and Unpacking
- Rakudo's Abstract Syntax Tree
- The REPL trick
- First day at YAPC::Europe 2013 in Kiev
- YAPC Europe 2013 Day 2
- YAPC Europe 2013 Day 3
- A new Perl 6 community server - call for funding
- New Perl 6 community server now live, accepting signups
- A new Perl 6 community server - update
- All Perl 6 modules in a box
- doc.perl6.org: some stats, future directions
- Profiling Perl 6 code on IRC
- Why is it hard to write a compiler for Perl 6?
- Writing docs helps you take the user's perspective
- Perl 6 Advent Calendar 2016 -- Call for Authors
- Perl 6 By Example: Running Rakudo
- Perl 6 By Example: Formatting a Sudoku Puzzle
- Perl 6 By Example: Testing the Say Function
- Perl 6 By Example: Testing the Timestamp Converter
- Perl 6 By Example: Datetime Conversion for the Command Line
- What is Perl 6?
- Perl 6 By Example, Another Perl 6 Book
- Perl 6 By Example: Silent Cron, a Cron Wrapper
- Perl 6 By Example: Testing Silent Cron
- Perl 6 By Example: Stateful Silent Cron
- Perl 6 By Example: Perl 6 Review
- Perl 6 By Example: Parsing INI files
- Perl 6 By Example: Improved INI Parsing with Grammars
- Perl 6 By Example: Generating Good Parse Errors from a Parser
- Perl 6 By Example: A File and Directory Usage Graph
- Perl 6 By Example: Functional Refactorings for Directory Visualization Code
- Perl 6 By Example: A Unicode Search Tool
- What's a Variable, Exactly?
- Perl 6 By Example: Plotting using Matplotlib and Inline::Python
- Perl 6 By Example: Stacked Plots with Matplotlib
- Perl 6 By Example: Idiomatic Use of Inline::Python
- Perl 6 By Example: Now "Perl 6 Fundamentals"
- Perl 6 Books Landscape in June 2017
- Living on the (b)leading edge
- The Loss of Name and Orientation
- Perl 6 Fundamentals Now Available for Purchase
- My Ten Years of Perl 6
- Perl 6 Coding Contest 2019: Seeking Task Makers
- A shiny perl6.org site
- Creating an entry point for newcomers
- An offer for software developers: free IRC logging
- Sprixel, a 6 compiler powered by JavaScript
- Announcing try.rakudo.org, an interactive Perl 6 shell in your browser
- Another perl6.org iteration
- Blackjack and Perl 6
- Why I commit Crud to the Perl 6 Test Suite
- This Week's Contribution to Perl 6 Week 5: Implement Str.trans
- This Week's Contribution to Perl 6
- This Week's Contribution to Perl 6 Week 8: Implement $*ARGFILES for Rakudo
- This Week's Contribution to Perl 6 Week 6: Improve Book markup
- This Week's Contribution to Perl 6 Week 2: Fix up a test
- This Week's Contribution to Perl 6 Week 9: Implement Hash.pick for Rakudo
- This Week's Contribution to Perl 6 Week 11: Improve an error message for Hyper Operators
- This Week's Contribution to Perl 6 - Lottery Intermission
- This Week's Contribution to Perl 6 Week 3: Write supporting code for the MAIN sub
- This Week's Contribution to Perl 6 Week 1: A website for proto
- This Week's Contribution to Perl 6 Week 4: Implement :samecase for .subst
- This Week's Contribution to Perl 6 Week 10: Implement samespace for Rakudo
- This Week's Contribution to Perl 6 Week 7: Implement try.rakudo.org
- What is the "Cool" class in Perl 6?
- Report from the Perl 6 Hackathon in Copenhagen
- Custom operators in Rakudo
- A Perl 6 Date Module
- Defined Behaviour with Undefined Values
- Dissecting the "Starry obfu"
- The case for distributed version control systems
- Perl 6: Failing Softly with Unthrown Exceptions
- Perl 6 Compiler Feature Matrix
- The first Perl 6 module on CPAN
- A Foray into Perl 5 land
- Gabor: Keep going
- First Grant Report: Structured Error Messages
- Second Grant Report: Structured Error Messages
- Third Grant Report: Structured Error Messages
- Fourth Grant Report: Structured Error Messages
- Google Summer of Code Mentor Recap
- How core is core?
- How fast is Rakudo's "nom" branch?
- Building a Huffman Tree With Rakudo
- Immutable Sigils and Context
- Is Perl 6 really Perl?
- Mini-Challenge: Write Your Prisoner's Dilemma Strategy
- List.classify
- Longest Palindrome by Regex
- Perl 6: Lost in Wonderland
- Lots of momentum in the Perl 6 community
- Monetize Perl 6?
- Musings on Rakudo's spectest chart
- My first executable from Perl 6
- My first YAPC - YAPC::EU 2010 in Pisa
- Trying to implement new operators - failed
- Programming Languages Are Not Zero Sum
- Perl 6 notes from February 2011
- Notes from the YAPC::EU 2010 Rakudo hackathon
- Let's build an object
- Perl 6 is optimized for fun
- How to get a parse tree for a Perl 6 Program
- Pascal's Triangle in Perl 6
- Perl 6 in 2009
- Perl 6 in 2010
- Perl 6 in 2011 - A Retrospection
- Perl 6 ticket life cycle
- The Perl Survey and Perl 6
- The Perl 6 Advent Calendar
- Perl 6 Questions on Perlmonks
- Physical modeling with Math::Model and Perl 6
- How to Plot a Segment of a Circle with SVG
- Results from the Prisoner's Dilemma Challenge
- Protected Attributes Make No Sense
- Publicity for Perl 6
- PVC - Perl 6 Vocabulary Coach
- Fixing Rakudo Memory Leaks
- Rakudo architectural overview
- Rakudo Rocks
- Rakudo "star" announced
- My personal "I want a PONIE" wish list for Rakudo Star
- Rakudo's rough edges
- Rats and other pets
- The Real World Strikes Back - or why you shouldn't forbid stuff just because you think it's wrong
- Releasing Rakudo made easy
- Set Phasers to Stun!
- Starry Perl 6 obfu
- Recent Perl 6 Developments August 2008
- The State of Regex Modifiers in Rakudo
- Strings and Buffers
- Subroutines vs. Methods - Differences and Commonalities
- A SVG plotting adventure
- A Syntax Highlighter for Perl 6
- Test Suite Reorganization: How to move tests
- The Happiness of Design Convergence
- Thoughts on masak's Perl 6 Coding Contest
- The Three-Fold Function of the Smart Match Operator
- Perl 6 Tidings from September and October 2008
- Perl 6 Tidings for November 2008
- Perl 6 Tidings from December 2008
- Perl 6 Tidings from January 2009
- Perl 6 Tidings from February 2009
- Perl 6 Tidings from March 2009
- Perl 6 Tidings from April 2009
- Perl 6 Tidings from May 2009
- Perl 6 Tidings from May 2009 (second iteration)
- Perl 6 Tidings from June 2009
- Perl 6 Tidings from August 2009
- Perl 6 Tidings from October 2009
- Timeline for a syntax change in Perl 6
- Visualizing match trees
- Want to write shiny SVG graphics with Perl 6? Port Scruffy!
- We write a Perl 6 book for you
- When we reach 100% we did something wrong
- Where Rakudo Lives Now
- Why Rakudo needs NQP
- Why was the Perl 6 Advent Calendar such a Success?
- What you can write in Perl 6 today
- Why you don't need the Y combinator in Perl 6
- You are good enough!
Sun, 20 Jun 2010
Physical modeling with Math::Model and Perl 6
Permanent link
Let's talk about physics. I'm a physicist by education and profession, so it might be not be too surprising. But I also want to talk about programming, so please bear with me.
When physicists try to understand a system, typically they first come up with a lot of equations, and then try to solve them. Unfortunately some of those equations are quite hard to solve. I've written a module that solves them numerically, and allows you to express the equations in very simple Perl 6 code.
Getting started
Let's start with a very simple model. As a prerequisite you need the Rakudo Perl 6 compiler (latest release or
current development version), and then use proto to proto install Math-Model
(which also installs its dependencies).
A first model: throwing a stone horizontally into the air
Let's start with an example (to be found in examples/vertical-throw.pl in the Math-Model repository, with small modifications to unconfuse the syntax hilighter used for this page).
It describes the path of stone thrown vertically into the air.
use v6; use Math::Model; my $m = Math::Model.new( derivatives => { y_velocity => 'y', y_acceleration => 'y_velocity', }, variables => { y_acceleration => { $:force / $:mass }, mass => { 1 }, # kg force => { -9.81 }, # N = kg m / s**2 }, initials => { y => 0, # m y_velocity => 20, # m/s }, captures => ('y', 'y_velocity'), ); $m.integrate(:from(0), :to(4.2), :min-resolution(0.2)); $m.render-svg('throw-vertically.svg', :title('vertical throwing'));
First we declare that we use Perl 6 (use v6;), and then we
load the module that does all the hard work, Math::Model.
Then comes the interesting part: the actual model. It starts by declaring
that the derivative of y (which is the name we use for the
current height of the stone) is called y_velocity. Likewise the
derivative of y_velocity is called
y_acceleration.
A derivative describes the rate of change of some other variables. Here is a short list of useful physical quantities and their derivatives:
| Quantity | Derivative |
|---|---|
| position | velocity |
| velocity | acceleration |
| acceleration | jerk |
| momentum | force |
| energy | power |
| charge | current |
Next in the model are formulas for some variables. We don't need to give
formulas for those values on the right-hand side of the derivatives
declarations (y and y_velocity), which we will call
integration variables. We just need formulas for the derivatives that
are not also integration variables, and for other variables we use in the
formulas.
You might remember from physics class that F = m * a, force is mass times acceleration. We use this formula for calculating the acceleration
y_acceleration => { $:force / $:mass },
The other variables are actually constants (but Math::Model doesn't distinguish those); mass is set to 1 kg, and the force to the -9.81 N that a mass of 1 kg experiences at the latitude where I live (Germany).
The programmer in you might ask what the heck the : in $:force
means. It's a variable that is automatically a named parameter to the current
block. Math::Model uses Signature
introspection to find out which variables such a block depends on, and
topologically sorts all variables into an order of execution that satisfies
all the dependencies.
Back to the physical model; all integration variables need an initial value, which are provided on the next few lines. The line
captures => ('y', 'y_velocity'),
tells Math::Model which variables to record while the simulation is running.
$m.integrate(:from(0), :to(4.2), :min-resolution(0.2)); $m.render-svg('throw-vertically.svg', :title('vertical throwing'));
Finally these two lines are responsible for running the actual simulation
(for the time t = 0s to t = 4.2s), and then write the resulting curves into
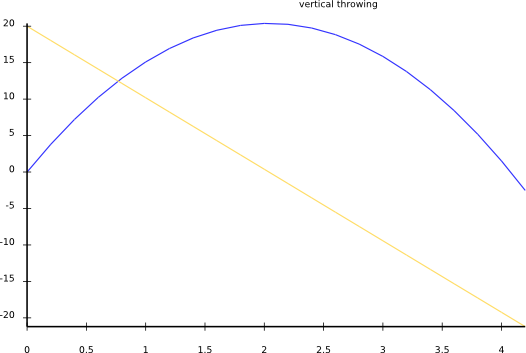
the file throw-vertically.svg. And here it is, without further
ado:
The blue line is the height (in meter), and the yellow line the velocity (in meter/second). Positive velocities mean that the stone is moving upwards, negative that it's moving downwards. After about 4 seconds the stone has the height with which it started, at a velocity of about -20m/s. You don't see any effect of the stone hitting the ground, because the model knows nothing about a ground located at a height of 0m. Just imagine the stone fell into a well or down a cliff, and thus can have negative height too.
Iterating: throwing a stone at an arbitrary angle
It gets a bit more involved when you consider not only the y direction, but also the x direction, and throw the stone at an arbitrary angle. Still the x and y axis are rather independent:
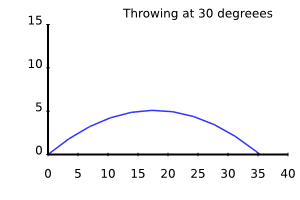
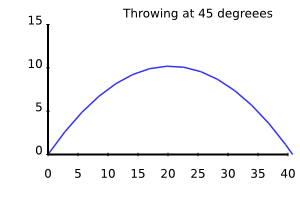
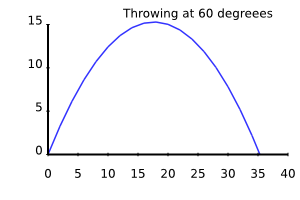
use v6; use Math::Model; for 30, 45, 60 -> $angle { my $m = Math::Model.new( derivatives => { y_velocity => 'y', y_acceleration => 'y_velocity', x_velocity => 'x', }, variables => { y_acceleration => { $:force / $:mass }, mass => { 1 }, # kg force => { -9.81 }, # N = kg m / s**2 x_velocity => { 20 * cos($angle, Degrees) } # m / s }, initials => { y => 0, # m y_velocity => 20 * sin($angle, Degrees), # m/s x => 0, # m }, captures => <y x>, ); $m.integrate(:from(0), :to(2 * 20 * sin($angle, Degrees) / 9.81), :min-resolution(0.2)); $m.render-svg("throw-angle-$angle.svg", :x-axis<x>, :width(300), :height(200), :title("Throwing at $angle degreees")); }
The x velocity stays approximately constant (we disregard air drag), and it's value is the cosine of the throwing angle times the initial, total velocity. The velocity in y direction is the sine of the throwing angle times the initial, total velocity.
As a trick to get nicer graphs in the end, I calculated the expected time
until it hits the ground (which I know to be 2 * v_y / a; this is
cheating, but it doesn't change the physics behind it).
Finally this time we don't want to have the elapsed time on the x axis, but
the actual position in x direction. That can be done with the
:x-axis<x> option.
(Note that I cheated to produces these charts; normally SVG::Plot, the module that produces these graphs, automatically scales the axis; I've manually suppressed that; if you try to out the example you'll see that the three charts look much the same, except for different axis scaling).
The maximum reach in x direction before hitting the ground is achieved at 45 degrees. For smaller angles it's not long enough in the air, and for larger angles too much of the velocity is "wasted" in the vertical direction, so the stone doesn't get very far.
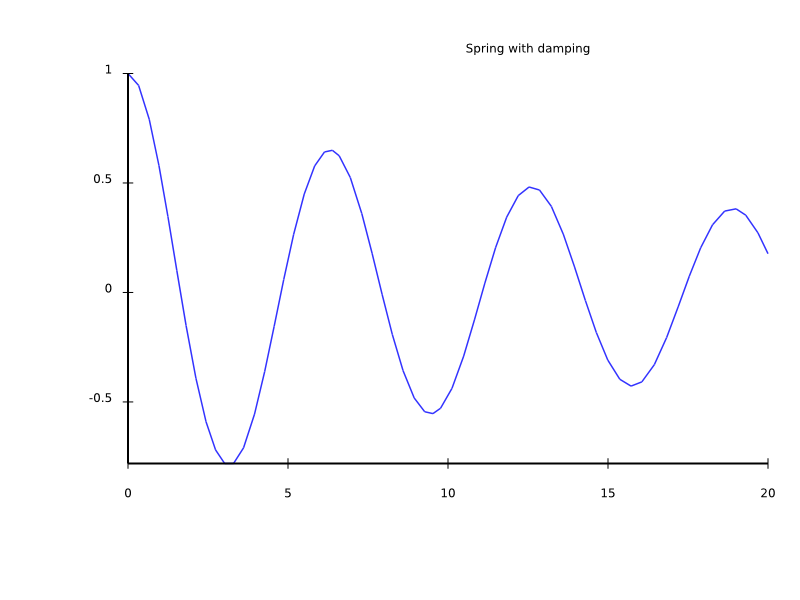
A third model: oscillating spring
Finally I want to present a third, simple model: a mass hanging down from a spring, this time including air drag. It doesn't show off any new features of Math::Model, but the result is a nice, oscillating curve.
use v6; use Math::Model; my $m = Math::Model.new( derivatives => { velocity => 'height', acceleration => 'velocity', }, variables => { acceleration => { $:force / $:mass }, mass => { 1 }, force => { - $:height - 0.2 * $:velocity * abs($:velocity)}, }, initials => { height => 1, velocity => 0, }, captures => <height>, ); $m.integrate(:from(0), :to(20), :min-resolution(1)); $m.render-svg('spring.svg', :title('Spring with damping'));
The air drag/damping is built into the formula for the force. It is proportional to the square of the velocity (making analytical solutions a nuisance), and always points in the opposite direction as the velocity.
Moving on
If you want to have some fun with Math::Model, here's a nice idea: You can simulate a mass attached to a spring, which can move freely in the xy plane. If you chose random initial values for the velocities in both directions, you can get non-periodic (chaotic?) trajectories in the xy plane.
(If you do, please send me the model so that I can also play with it :-))
A personal note
Ever since I've used the simulation tool "stella" in school (must have been year 2002 or so), I've wanted to write something similar. Math::Model is it. It was quite fun to implement in Perl 6. The only drawback is that it's quite slow.